Research – mathlab

I work mostly on combinatorics related to algebraic geometry and representation theory, though I also have an abiding interest in algorithmic number theory. Most of my papers are on symmetric spaces and their embeddings, which provide a nice context for generalizing Coxeter group combinatorics to certain kinds of involutions or “clans.” I also have work on Kazhdan-Lusztig polynomials, poset topology, and elementary number theory. More recently, I am working on methods of computing Kronecker coefficients in the combinatorial representation theory of the symmetric group, and other group projects involving Kohnert diagram posets and chromatic symmetric functions. Below are links and descriptions for some of my papers.

Someday, I’m hoping works around themes such as saturation, unimodality, functional digraphs, diagrammatic calculus (projects at varying stages of completion with diverse collaborators) will appear here too. If any of these topics interest you, feel free to get in touch.

Kronecker coefficients in the (p,q,2)-case via polytopes, with Ernesto Vallejo (coming soon): We recover and extend several results about Kronecker coefficients when one of the partitions has two parts using certain polytopes.

Lexicographic shellability of sects, with Néstor Díaz Morera, 2023: We show that the sects of the type 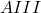$AIII$ symmetric variety are EL-shellable posets. We started this project attempting to show that the full Bruhat poset of Borel orbits on the symmetric variety (i.e. the poset of (p,q)-clans) was lexicographically shellable, but ran into some obstacles that we couldn’t see how to overcome, even using more flexible tools from the shellability toolkit like CL-labellings or CC-labellings. We still believe it to be the case that Bruhat posets on homogeneous spaces like symmetric varieties should be shellable. But we found it a nice consolation to use a bijection between sect orbits and rook placements in partition shapes, along with ideas from work of our adviser Mahir Can to obtain this result. It also surprised us that, somehow, this seems to be the time shellability of the poset of matrix Schubert varieties in rectangular matrices has been explicitly established.

Kazhdan-Lusztig polynomials for 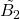$\tilde{B_2}$ , with Karina Batistelli and David Plaza, 2021: We calculate recursive and explicit formulas for the canonical basis of the Hecke algebra for an affine Weyl group of type 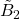$\tilde{B}_2$ , as well as descriptions of lower intervals of the Bruhat order on this group. Combining these pieces of information, one can (more) easily extract Kazhdan-Lusztig polynomials 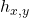$h_{x,y}$ for pairs of elements in this group. These are the first such comprehensive calculations for a Coxeter group in which the 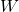$W$ -graph is not locally finite. (Journal of Pure and Applied Algebra, 2023)

Ternary arithmetic, factorization, and the class number one problem, 2020: A commutative ternary “multiplication” operation on natural numbers can be defined by counting lattice points in the hexagonal lattice. It turns out that the “prime” numbers for this multiplication correspond to certain imaginary quadratic fields with unique factorization. I also describe some simple algorithms for primality testing and integer factorization. (It turns out that the factorization algorithm described is essentially the same as what is sometimes called “Kraitchik’s algorithm.”) This grew out of research I did for my master’s thesis. (Revista Colombiana de Matemáticas, 2022)

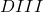
DIII clan combinatorics for the orthogonal Grassmannian, with Ozlem Ugurlu, 2019: We provide some bijective combinatorics for the parameter set of Borel orbits in a symmetric space of type 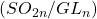$DIII$ $(SO_{2n}/GL_n)$ , which consists of clans with certain conditions. For clarity, we somewhat uncreatively called these “DIII clans,” though in retrospect I sort of wish we had gone with “spinor clans,” since part of the fun is once again identifying the sects corresponding to Schubert cells of the connected component of the even orthogonal Grassmannian which identifies with what is often called the spinor variety. Some other neat coincidences with rook placements, set partitions and weighted Delannoy paths show up as well. (Australasian Journal of Combinatorics, 2021)

Sects and lattice paths over the Lagrangian Grassmannian, with Ozlem Ugurlu, 2019: We enumerate and biject the clans parametrizing the 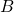$B$ -orbits classical symmetric space 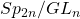$Sp_{2n}/GL_n$ to certain restricted involutions and weighted Delannoy paths. We hoped to use the Delannoy paths to eventually describe the “Bruhat” or closure order on the clans, but this turned out to be unnecessary after discovering work of Gandini-Maffei. We were able to describe the sects and find a nice “big sect” coincidence with another Bruhat poset of partial involutions. (Electronic Journal of Combinatorics, 2020)

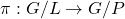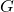Sects, with Mahir Can, 2018: We describe local trivializations that give an affine bundle structure to the natural projection map $\pi: G/L \to G/P$ where $G$ is a reductive complex linear algebraic group and 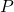$P$ is a parabolic subgroup with Levi factor 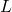$L$ . This gives a cell decomposition of the affine variety 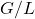$G/L$ which allows identification of its cohomology and Chow rings with those of 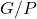$G/P$ . The details of the case 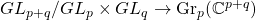$GL_{p+q}/GL_p \x GL_q\to \text{Gr}_p(\C^{p+q})$ are spelled out, combinatorially describing the collections of clans that constitute each cell, which we call a sect. (Journal of Algebra, 2020)

A filtration on equivariant Borel-Moore homology, with Mahir Can and Yildiray Ozan, 2018: We find some splittings of long exact sequences for relative (equivariant) Borel-Moore homology and Chow groups that allow us to obtain direct sum decompositions over the orbits for varieties with finitely many 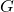$G$ -orbits. In particular, this applies to wonderful embeddings of spherical homogeneous spaces 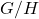$G/H$ including symmetric varieties. Together with results of the “Sects” paper, one has a complete description of the cohomology of symmetric spaces of Hermitian type and their embeddings. (Forum of Mathematics, Sigma, 2019).